Image of Rburtonresearch from wikipedia
Què és el so? El so és una ona esfèrica provocada pels canvis de pressió a les capes d'aire que envolten el punt material causant del so. Quan parlem de pressió ens referim al mateix que entenem per pressió atmosfèrica.
Si un objecte material, a causa d'un cop, d'una vibració, pressiona la capa d'aire que té més a prop, aquesta pressió es comunica cíclicament a les capes immediatament més properes i es propaga en forma d'ones esfèriques. Les següents imatges t'ajudaran a comprendre-ho.
El centre dels cercles de la següent imatge és el punt on es produeix el so: el punt 1 (en groc). Aquest punt 1 té una pressió de 0,94 bars.
La capa d'aire que té just al costat és la 2 (en groc) i per la proximitat que té amb la 1, se li comunica una pressió de 0,93 bars.
La següent és la 3, i tindrà una pressió de 0,92 bars.
La següent és la 4, i tindrà una pressió de 0,91 bars.
La següent la 5 i tindrà una pressió de 0,9 bars.
La següent la 6, i fixa't que torna a pujar la pressió, valdrà 0,91... i així successivament i infinitament.
Nosaltres hem dibuixat fins a la capa d'aire 17, però a la realitat continuaria.
La capa d'aire que té just al costat és la 2 (en groc) i per la proximitat que té amb la 1, se li comunica una pressió de 0,93 bars.
La següent és la 3, i tindrà una pressió de 0,92 bars.
La següent és la 4, i tindrà una pressió de 0,91 bars.
La següent la 5 i tindrà una pressió de 0,9 bars.
La següent la 6, i fixa't que torna a pujar la pressió, valdrà 0,91... i així successivament i infinitament.
Nosaltres hem dibuixat fins a la capa d'aire 17, però a la realitat continuaria.
També és veritat que com més lluny del punt on s'ha originat el so està la capa d'aire, la variació de pressió aniria disminuint en els valors dels bars, baixaria l'amplitud d'ona, i això equivaldria a que l'ona sonora se sentiria més fluixa, fins que acabaria per apagar-se.
I tot això que hem explicat, i que està dibuixat a la imatge següent, passaria en un instant, que anomenem l'instant 0.
A l'instant següent, que en aquest exemple seria el instant 2,27 milisegons, continuaria la vibració, però el valor de la pressió s'hauria traslladat una capa cap endins.
És a dir, a la capa 2, a on abans hi havia una pressió de 0,93 bars, ara n'hi haurà 0,92 (que era el que hi havia abans a la capa 3).
A la capa 3, a on abans hi havia una pressió de 0,92, ara hi haurà una pressió de 0,91 (que era el que abans hi havia a la capa 1),
i aixi successivament, tal com pots veure al següent dibuix.
Compara els dos dibuixos, el de dalt i el de baix, i assegura't que ho entens.
És a dir, a la capa 2, a on abans hi havia una pressió de 0,93 bars, ara n'hi haurà 0,92 (que era el que hi havia abans a la capa 3).
A la capa 3, a on abans hi havia una pressió de 0,92, ara hi haurà una pressió de 0,91 (que era el que abans hi havia a la capa 1),
i aixi successivament, tal com pots veure al següent dibuix.
Compara els dos dibuixos, el de dalt i el de baix, i assegura't que ho entens.
Si ho posem en forma de taula, a la taula de sota tenim totes les capes d'aire a l'instant 0 i la seva pressió en bars:
I ara les mateixes capes, a l'instant següent, és a dir 2,27 milisegons després:
I al tercer instant que observem, és a dir a l'instant 4,54 milisegons, ha tornat ha canviar ordenadament el valor de la pressió, ben bé com si la pressió d'una capa, hagués passat a la del costat:
I també veiem que si ens movem per l'espai, dins d'un mateix instant de temps, a cada capa d'aire hi ha una pressió diferent, i movent-nos endavant a mesura que ens allunyem del punt a on s'ha produït el so, aniríem pujant i baixant en els valors de la pressió de l'aire.
I què passa si no ens movem d'una mateixa capa d'aire, per exemple de la capa 3 del dibuix, i anem mesurant la pressió de l'aire d'aquesta capa 3 que hi va havent al llarg dels instants?
Doncs tal com veus a la taula superior, es produeix la mateixa variació cíclica de la pressió de l'aire, que oscil·la entre els mateixos valors. En aquest cas 0,9 bars de mínim i 0,94 de màxim.
Primer baixa de 0,93, a 0,92.
I al següent instant de 0,92 a 0,91,
i així successivament.
Però quan arriba a 0,9, comença a pujar de nou, de 0,9 a 0,91, després de 0,91 a 0,92, després de 0,92 a 0,93.... i així successivament, fins a un màxim de 0,94.
Primer baixa de 0,93, a 0,92.
I al següent instant de 0,92 a 0,91,
i així successivament.
Però quan arriba a 0,9, comença a pujar de nou, de 0,9 a 0,91, després de 0,91 a 0,92, després de 0,92 a 0,93.... i així successivament, fins a un màxim de 0,94.
Això ho hem observat a la capa 3, però el mateix passa a cada capa d'aire.
Aquest fenomen que acabem d'analitzar, és el so.
Quan aquest canvi cíclic de la pressió de les capes d'aire es va expandint en forma d'ones esfèriques cap a totes direccions, arriba a la nostra orellà, fa vibrar el nostre timpà, que excita el nervi òptic, i aquest envia al nostre cervell la informació del so en forma de petitíssims corrents elèctrics. Dins el nostre cervell hi ha una zona que té la missió de convertir aquesta informació que arriba en sensació de so a la consciència.
Valors importants que cal comprendre en una ona sonora
Amplitud: l'amplitud és la diferència entre el valor més alt de pressió que agafa una capa, i el valor més baix. Com més grossa és l'amplitud, més fort se sent el so. L'amplitud, per tant, va lligada al volum del so.
Freqüència: La freqüència és el nombre d'oscilacions completes d'una ona que succeeixen en un segon. Una oscil·lació completa de l'ona sonora, en el cas de l'exemple de dalt, seria des que la pressió d'una capa d'aire determinada val 0,94 bars, fins que torna a valer 0,94 bars. Aleshores, per saber la freqüència hauríem de comptar quantes vegades en un segon la pressió varia de 0,94 bars fins a 0,94 bars, passant per tots els valors intermitjos. Aquesta xifra la donaríem en Hertzs.
La gràfica següent reflecteix la variació de pressió a la capa 1 on s'origina el so al llarg del temps.Tal com veus, la oscil·lació completa s'aproxima a una mena de V. Aleshores la freqüència seria el nombre de "V" que hi hauria en un segon, i el valor es donaria en Hertz.
La freqüència va associada al to, el que en música anomenem notes musicals. La diferència entre un to i un altre, és a dir, el que fa que una nota sigui diferent a una altra, és la freqüència. Com més freqüència, més aguda és la nota. Com menys freqüència, més greu és la nota.
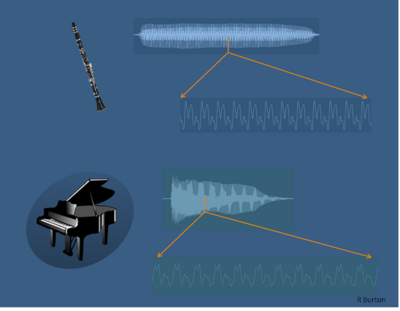
Harmònics i Timbre: Normalment, els sons no són purs, són un barreja de diferents ones. En aquesta barreja d'ones, si pensem en la veu humana o en el so d'un instrument, sempre hi ha una ona principal, i unes altres d'amplitud molt més baixa, però amb la mateixa freqüència que l'ona principal. Aquestes ones que acompanyen a l'ona principal, però que tenen una amplitud més baixa, s'anomenen harmònics, i gràcies als harmònics escoltem diferent el so d'un violoncel del so d'un piano, del so de la veu humana, ni que tots tres interpretin la mateixa nota amb la mateixa amplitud. Això que ens permet diferenciar diferents instruments s'anomena TIMBRE, i depèn dels harmònics.
Per avui ja hem explicat prou conceptes. Un altre dia seguim.
ACTIVITATS (realitza-les al teu blog)
1.- Calcula l'amplitud i la freqüència en l'ona de l'exemple, a partir de la gràfica que relaciona els bars amb els milisegons (on surt la "V" de la forma d'ona) Penja les teves deduccions i el raonament que fa amb el resultat al teu blog.
2.- Cerca quina freqüència en Hertz tenen les següents notes musicals: Do, re, mi, fa, #fa, sol, #sol, la, si. Escull una octava qualsevol. Penja-ho al blog.
3.- Quina és la freqüència mínima i màxima d'una ona sonora que un ésser humà pot escoltar? Podria escoltar l'ona de l'exemple del blog?
4.- A l'exemple del blog, si en comptes d'oscil·lar entre 0,9 bars i 0,94 bars, oscil·lés entre 0,7 bars i 1,14 bars, quina diferència sentiries respecte la primera situació, suposant que l'ona es pogués sentir?
Et recomano que visitis la següent web i a banda de llegir-la observis els gifs i els dibuixos:
http://www.physicsclassroom.com/class/sound/u11l1c.cfm
Quan aquest canvi cíclic de la pressió de les capes d'aire es va expandint en forma d'ones esfèriques cap a totes direccions, arriba a la nostra orellà, fa vibrar el nostre timpà, que excita el nervi òptic, i aquest envia al nostre cervell la informació del so en forma de petitíssims corrents elèctrics. Dins el nostre cervell hi ha una zona que té la missió de convertir aquesta informació que arriba en sensació de so a la consciència.
Valors importants que cal comprendre en una ona sonora
Amplitud: l'amplitud és la diferència entre el valor més alt de pressió que agafa una capa, i el valor més baix. Com més grossa és l'amplitud, més fort se sent el so. L'amplitud, per tant, va lligada al volum del so.
Freqüència: La freqüència és el nombre d'oscilacions completes d'una ona que succeeixen en un segon. Una oscil·lació completa de l'ona sonora, en el cas de l'exemple de dalt, seria des que la pressió d'una capa d'aire determinada val 0,94 bars, fins que torna a valer 0,94 bars. Aleshores, per saber la freqüència hauríem de comptar quantes vegades en un segon la pressió varia de 0,94 bars fins a 0,94 bars, passant per tots els valors intermitjos. Aquesta xifra la donaríem en Hertzs.
La gràfica següent reflecteix la variació de pressió a la capa 1 on s'origina el so al llarg del temps.Tal com veus, la oscil·lació completa s'aproxima a una mena de V. Aleshores la freqüència seria el nombre de "V" que hi hauria en un segon, i el valor es donaria en Hertz.
La freqüència va associada al to, el que en música anomenem notes musicals. La diferència entre un to i un altre, és a dir, el que fa que una nota sigui diferent a una altra, és la freqüència. Com més freqüència, més aguda és la nota. Com menys freqüència, més greu és la nota.
Harmònics i Timbre: Normalment, els sons no són purs, són un barreja de diferents ones. En aquesta barreja d'ones, si pensem en la veu humana o en el so d'un instrument, sempre hi ha una ona principal, i unes altres d'amplitud molt més baixa, però amb la mateixa freqüència que l'ona principal. Aquestes ones que acompanyen a l'ona principal, però que tenen una amplitud més baixa, s'anomenen harmònics, i gràcies als harmònics escoltem diferent el so d'un violoncel del so d'un piano, del so de la veu humana, ni que tots tres interpretin la mateixa nota amb la mateixa amplitud. Això que ens permet diferenciar diferents instruments s'anomena TIMBRE, i depèn dels harmònics.
Per avui ja hem explicat prou conceptes. Un altre dia seguim.
ACTIVITATS (realitza-les al teu blog)
1.- Calcula l'amplitud i la freqüència en l'ona de l'exemple, a partir de la gràfica que relaciona els bars amb els milisegons (on surt la "V" de la forma d'ona) Penja les teves deduccions i el raonament que fa amb el resultat al teu blog.
2.- Cerca quina freqüència en Hertz tenen les següents notes musicals: Do, re, mi, fa, #fa, sol, #sol, la, si. Escull una octava qualsevol. Penja-ho al blog.
3.- Quina és la freqüència mínima i màxima d'una ona sonora que un ésser humà pot escoltar? Podria escoltar l'ona de l'exemple del blog?
4.- A l'exemple del blog, si en comptes d'oscil·lar entre 0,9 bars i 0,94 bars, oscil·lés entre 0,7 bars i 1,14 bars, quina diferència sentiries respecte la primera situació, suposant que l'ona es pogués sentir?
Et recomano que visitis la següent web i a banda de llegir-la observis els gifs i els dibuixos:
http://www.physicsclassroom.com/class/sound/u11l1c.cfm
Image of Rburtonresearch from wikipedia









Cap comentari:
Publica un comentari a l'entrada